In diesem Teil geht es um das bewegen, Drehen und Kombinieren von Objekten .
Zuerst erzeugen wir wieder einen Würfel. Das solltet ihr inzwischen können.
Der Würfel ist ja mit einer Ecke im Nullpunkt des Koordinatensystems platziert. Wenn wir den Würfel aber an einer anderen Stelle benötigen, müssen wir ihn verschieben. Der dafür benötigte Befehl heißt “translate”. Er wird vor das zu verschiebende Objekt geschrieben und benötigt, genau wie ein Kubus drei Werte, je für X Y und Z Richtung. Das sieht also beispielsweise so aus:
translate([5,0,0])cube(10);
Das Ergebnis ist dann
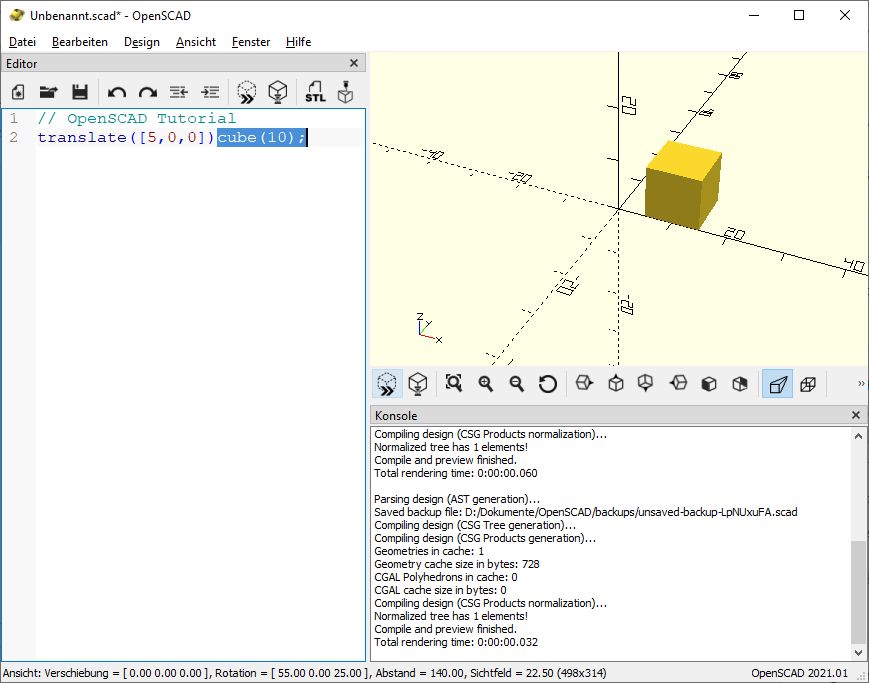
ein um 5 mm entlang der X- Achse verschobener Würfel mit 10 mm Kantenlänge. So lange wie wir nur ein einziges Objekt haben, spielt es eigentlich keine Rolle, wo das Objekt platziert ist. Das ändert sich aber schlagartig, wenn man mehr als ein Objekt benötigt.
Wir erzeugen nun einen Würfel mit 10 mm Kantenlänge und eine Kugel mit 10 mm Durchmesser. Das sollte kein Problem sein, haben wir beides schon gemacht. Um das aktuelle Problem besonders zu verdeutlichen, platzieren wir den Würfel Zentriert, also mit center=true als Parameter.
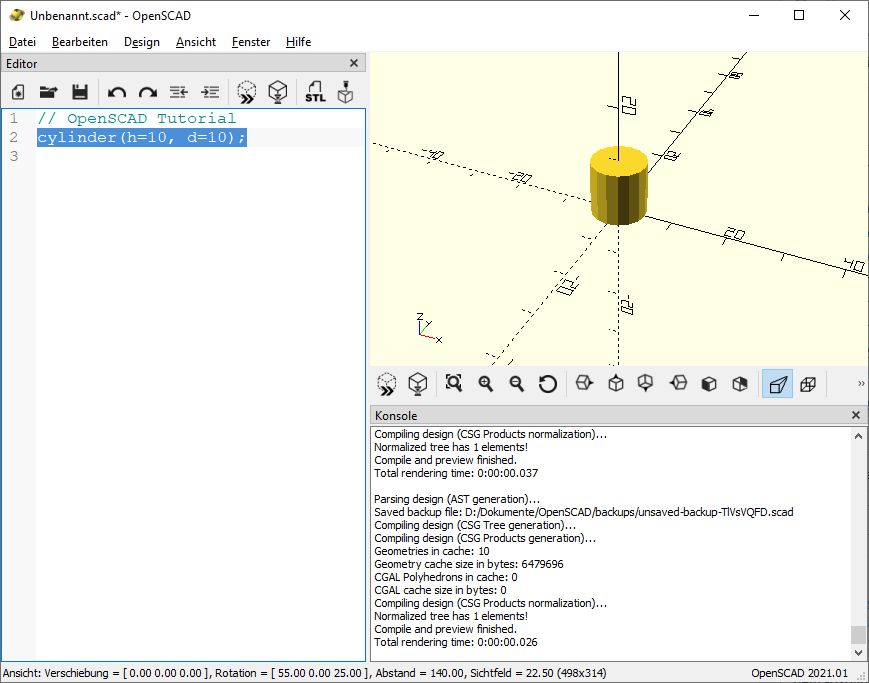
cube(10,true);
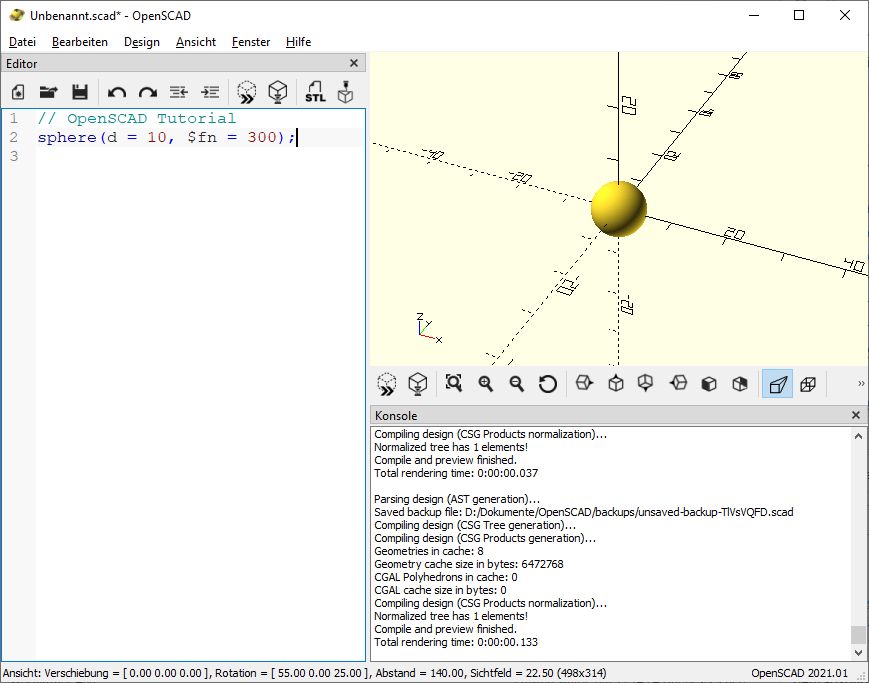
sphere(d=10, $fn=300);
Das Ergebnis ist zum einen erstaunlich, zum anderen aber auch nachvollziehbar:
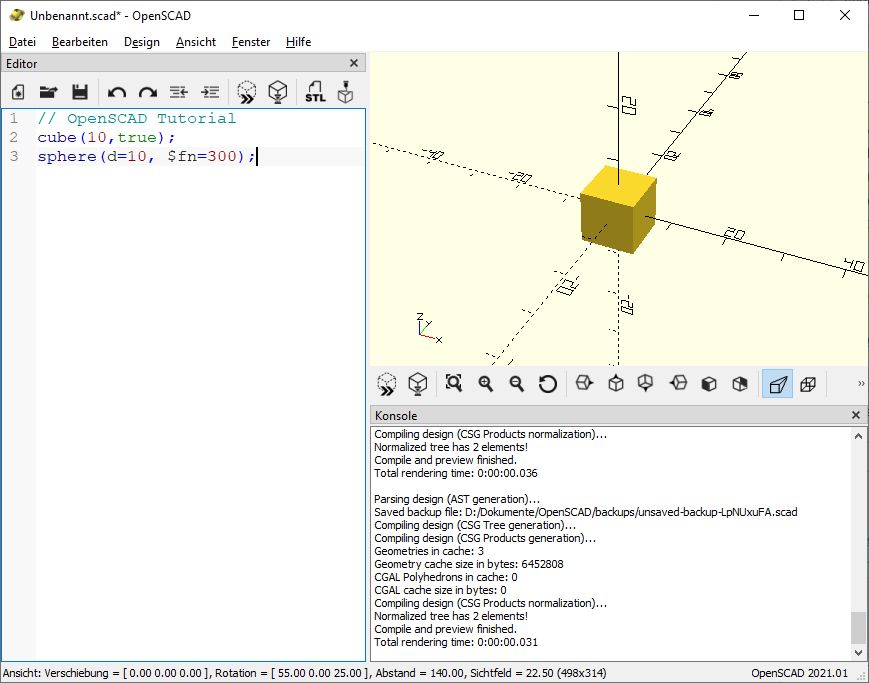
Wir sehen nur den Würfel, von der Kugel fehlt jede Spur. Denkt man mal kurz darüber nach, ist schnell klar, die Kugel ist deswegen nicht zu sehen, weil sie vollständig im Inneren des Würfels liegt.
Hier kommt jetzt der translate Befehl zum Zuge. Wir bewegen die Kugel einfach um 10 mm entlang der Z Achse:
cube(10,true);
translate([0,0,10])sphere(d=10, $fn=300);
und schon taucht sie wie von Zauberhand auf und thront auf dem Würfel.
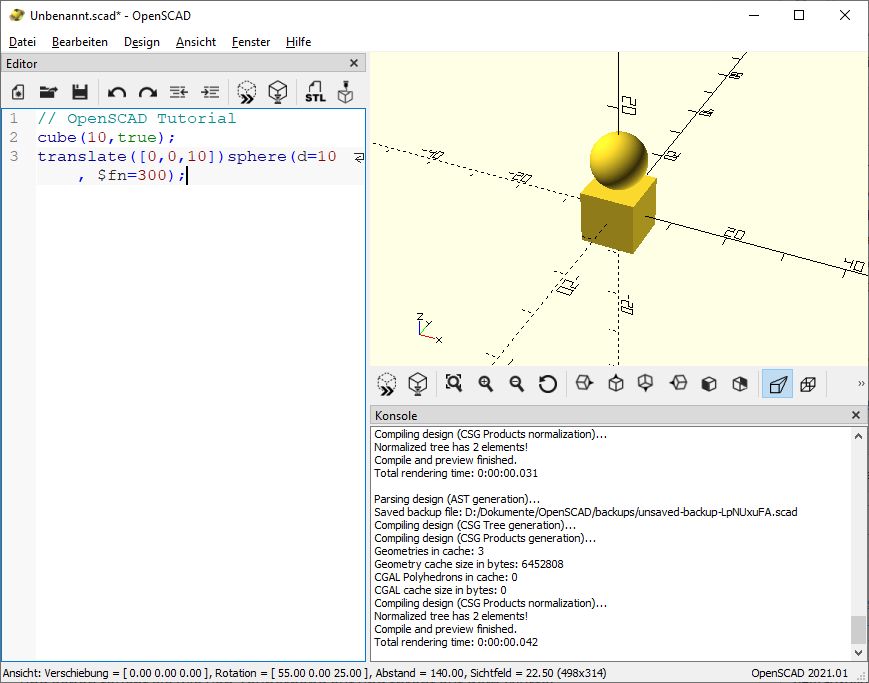
Man muss die Kugel natürlich nicht genau auf den Würfel setzen. Man kann sie darüber oder daneben platzieren oder auch partiell im Würfel versenken. Natürlich kann man auch den Würfel auf die Kugel setzen, wenn man möchte. Zur Verdeutlichung heben wir die Kugel mal nur um 5 mm an:
cube(10,true);
translate([0,0,5])sphere(d=10, $fn=300);
Das liefert dann dieses Ergebnis:
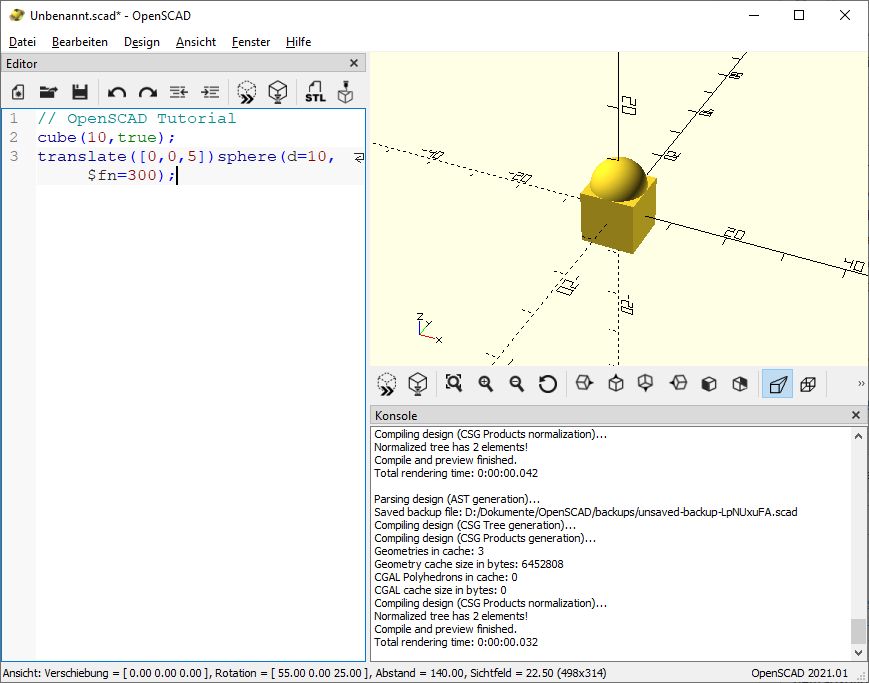
Und schon haben wir einen Buzzer konstruiert.
Bei einer Kugel spielt die Orientierung im Raum ja keine Rolle, bei einem Kubus aber durchaus. Um Objekte zu rotieren (englisch rotate) kommt, welch Wunder, der Befehl rotate zum Einsatz. Die Syntax ist praktisch identisch zu translate, nur das man bei rotate eben die Rotation in° angibt
rotate([45,45,45])cube(10);
Ergibt:
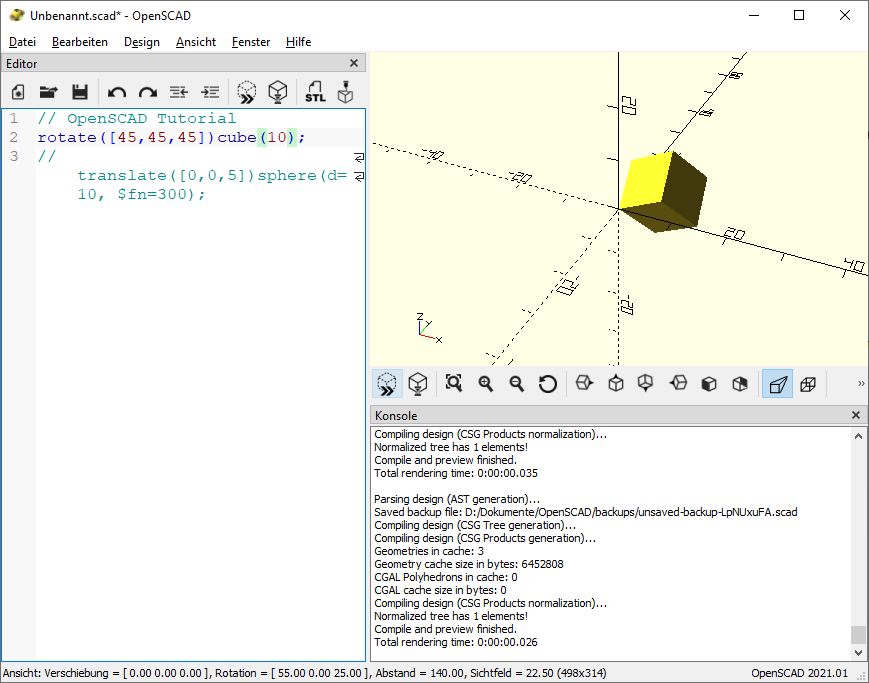
Man kann sehen, das ich die Kugel aus kommentiert habe (also die Zeile mit // eingeleitet habe). Somit wird sie ignoriert und ich kann sie im nächsten Schritt schnell wieder einbauen, ohne alles neu tippen zu müssen…
Nun binden wir die Kugel wieder ein und platzieren sie genau auf die eine Ecke des Würfels. dafür braucht man ein wenig Geometrie- Kenntnisse aus der Schule. Schon mal was von PI gehört? Klar, da war doch was… Irgendwas mit Kreis und 3,14.. Also versuchen wir das einfach mal:
rotate([45,45,45])cube(10);
translate([-3.14,-3.14,-3.14])sphere(d=10, $fn=300);
Erstaunlicherweise kommt dabei das raus:
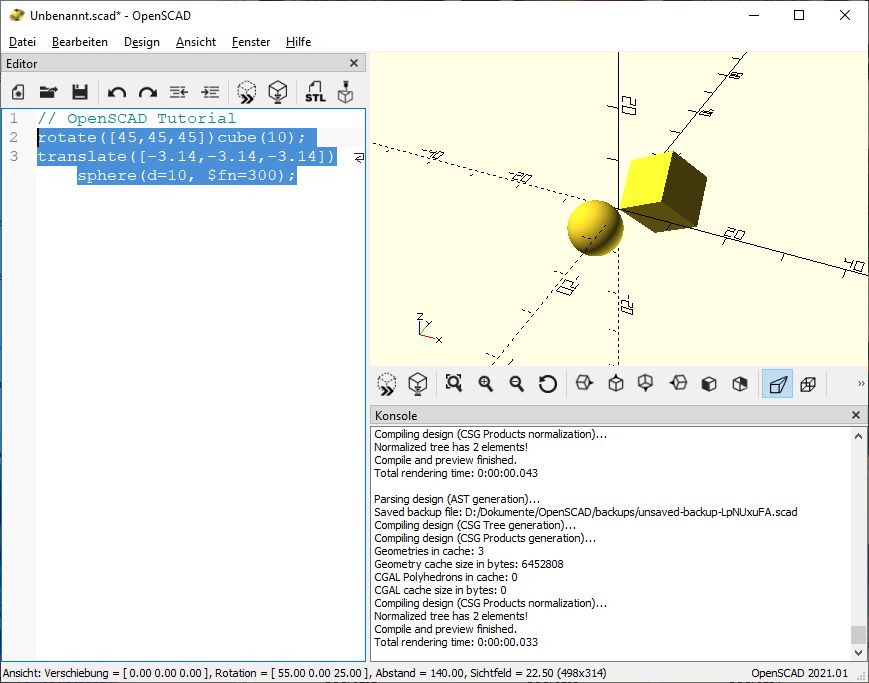
ich gebe ja zu, ich habe es vorher ausprobiert und deswegen die 10 mm Durchmesser gewählt. Bei 20 mm Durchmesser hätte ich -6,28 nehmen müssen, usw… Eine kurze Formel dafür wäre (d/10) * 3,14
So könnte man das Objekt aber nicht drucken, da sich Würfel und Kugel nur in einem einzigen winzigen Punkt berühren. Man müsste entweder die Verbindung durch zusätzliche Objekte, z.B. einen Zylinder verstärken oder man “versenkt” die Kugel teilweise im Würfel:
rotate([45,45,45])cube(10);
translate([-2.5,-2.5,-2.5])sphere(d=10, $fn=300);
Mit folgendem Ergebnis:
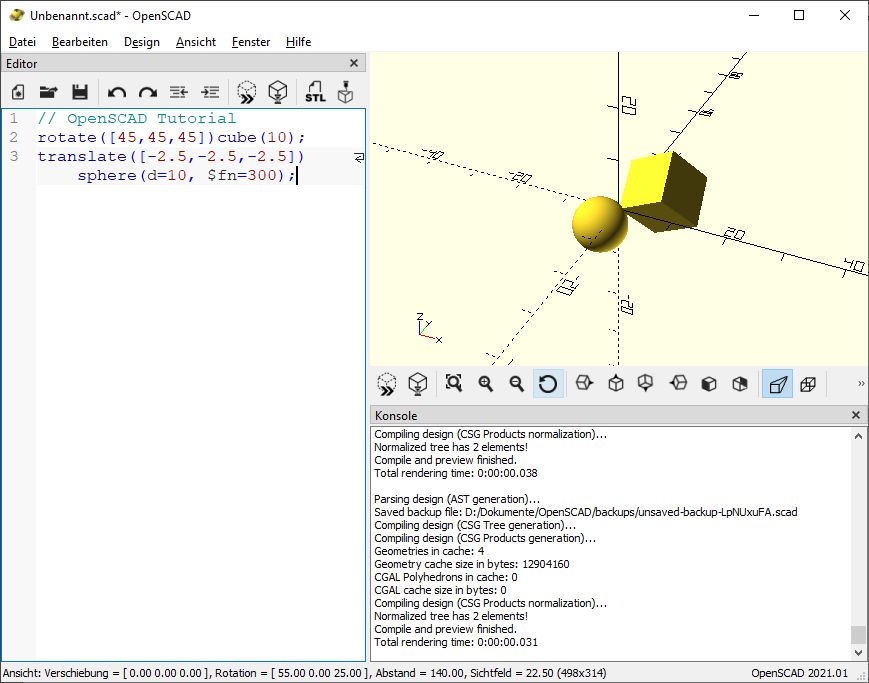
Nun ist die Verbindung zwischen Kugel und Würfel erheblich stabiler.
Eine weitere Operation muss ich noch behandeln, bevor wir tatsächlich anfangen können, etwas “Produktives” zu machen. Stellen wir uns mal vor, wir möchten gerne Löcher in der Grundplatte unserer Servo- Halterung haben, um sie leicht anschrauben zu können.
Also konstruieren wir zunächst die Grundplatte selbst. Sie soll in diesem Beispiel 65 mm lang und 30 mm breit sein, sowie 3 mm dick. Die Maße habe ich für ein Modelcraft RS-2 Servo, welche es vor Jahren mal bei Conrad im Angebot für 2€ das Stück gab, ausgewählt. Dazu benötigen wir was? Natürlich einen Kubus mit [65,30,3] als Parameter.
cube([65,30,3]);
Da unsere Platte nun über das Sichtfeld hinaus ragt, können bzw. müssen wir die Ansicht verschieben oder verkleinern. Das macht man mit der Maus. Je nach dem, ob man rechts oder links geklickt hält, verändert sich die Position und/oder Perspektive. Mit dem Mausrad kann man hinein oder hinaus zoomen.
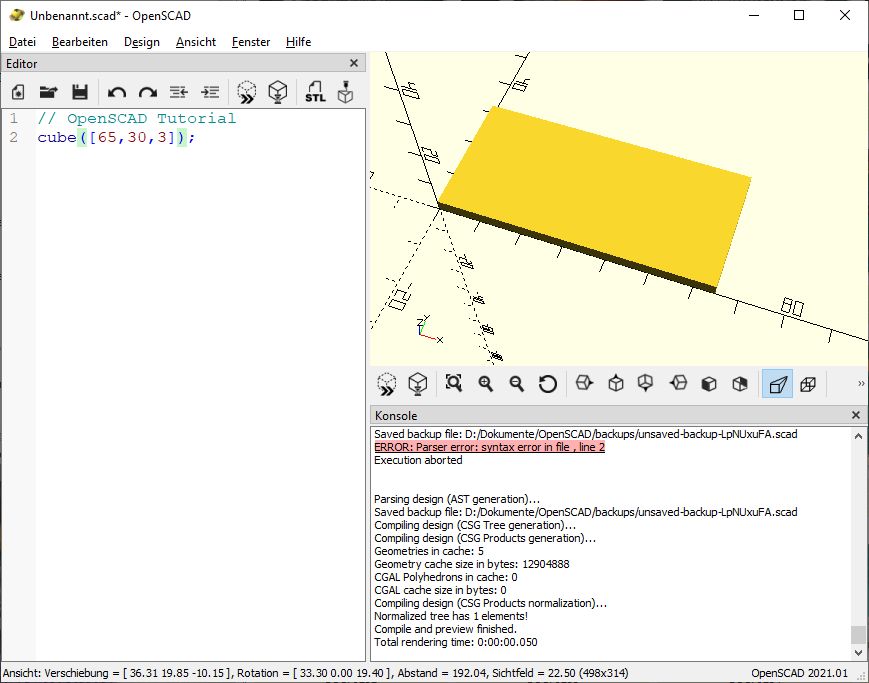
Viele der Knöpfe unterhalb der 3D Ansicht dienen dazu, die Position bzw. Perspektive zu verändern. Wenn ihr euch dabei völlig verheddert, keine Sorge. Dafür gibt es einen “Panik- Knopf” und zwar den Kreis mit dem Pfeil drin, der sechste Knopf von links. Wenn ihr da drauf klickt, wird die Ansicht wieder auf Normal eingestellt…
Ich habe in diesem Fall eine Ansicht ziemlich von Oben gewählt, weil uns das gleich beim Erzeugen der Löcher hilft.
Das ist also unsere Grundplatte. Nun müssen wir Löcher hinein bohren. Natürlich virtuell in 3D und nicht später real am fertig gedruckten Objekt (was theoretisch auch funktionieren würde).
Dazu verwenden wir nun Zylinder, die wir von der Grundplatte abziehen werden. Der Zylinder soll 3,2 mm Durchmesser haben damit 3 mm Schrauben problemlos durchpassen. Und er muss etwas höher sein, als die eigentliche Grundplatte, damit die Öffnung auch tatsächlich vollständig wird.
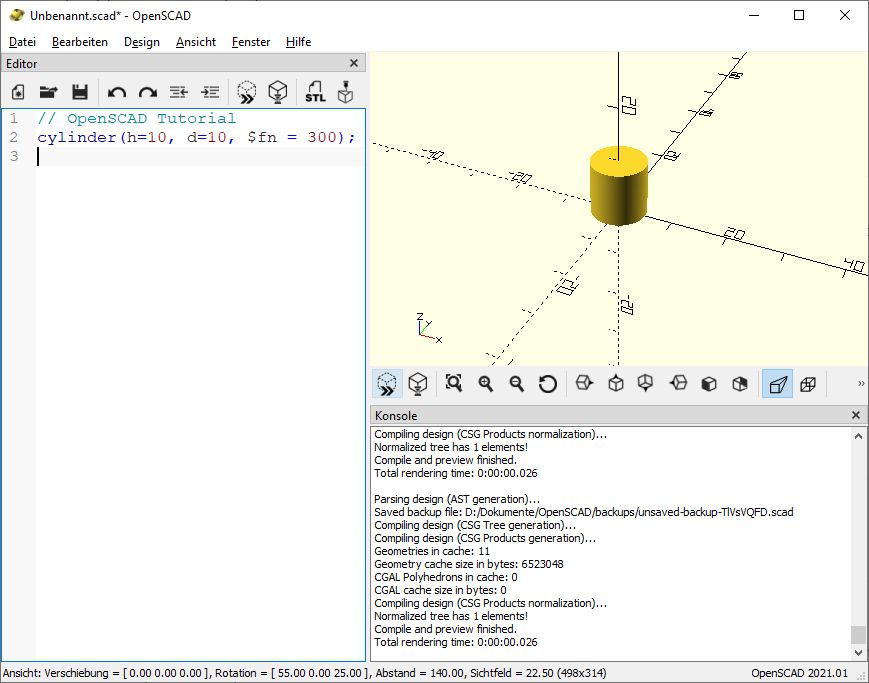
cylinder(h=5, d=3.2, $fn = 300);
Das fügen wir nun unserem “Programm” hinzu.
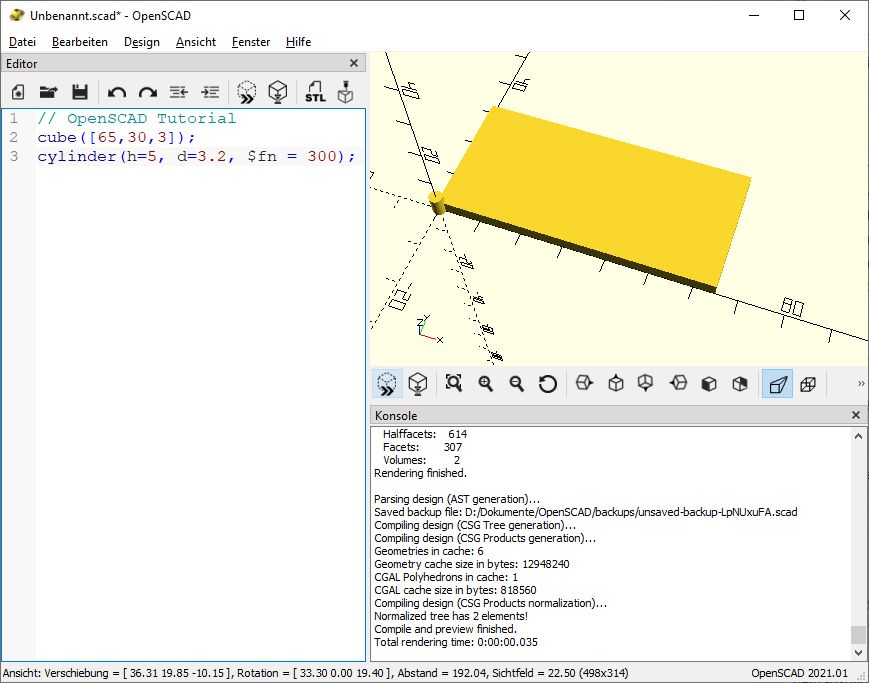
Diesen Zylinder werden wir später von der Grundplatte abziehen. Zunächst muss er aber erst mal an die richtige Stelle verschoben werden. In Z Richtung verschieben wir ihn um -1, damit er auch sicher komplett durch die Grundplatte ragt. Deswegen haben wir ihn ja 5 mm hoch und nicht 3 mm hoch gemacht. In X und Y Richtung verschieben wir ihn um 4 mm, also
translate([4,4,-1])cylinder(h=5, d=3.2, $fn = 300);
Nun ist der Zylinder richtig platziert:
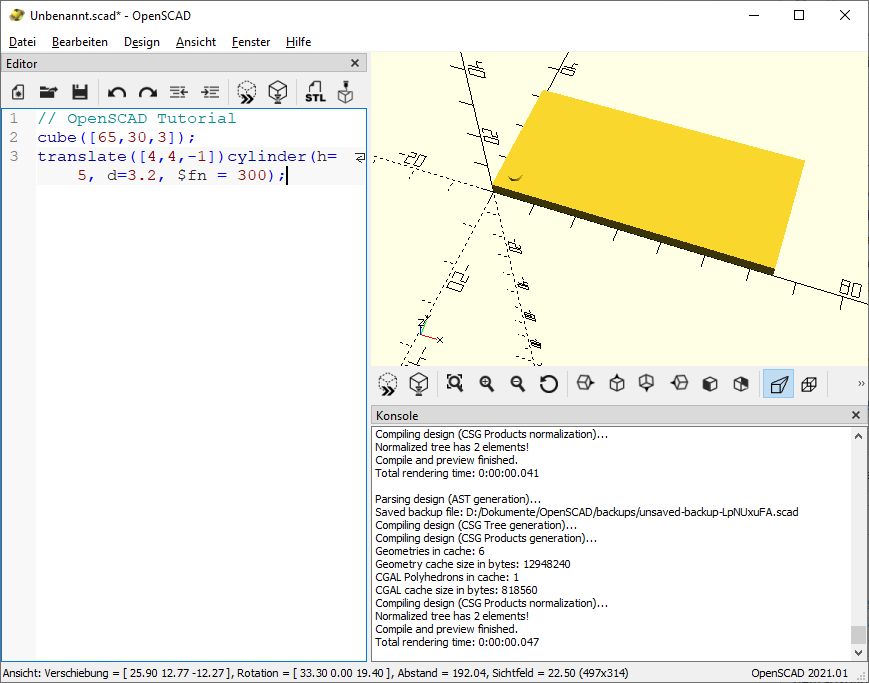
Erinnert ein ganz klein wenig an Lego, oder? Jetzt müssen wir den Zylinder “nur” noch von der Grundplatte abziehen.
Dafür gibt es den Befehl “difference”. Da wir es hier mit einer Boolschen Operation zu tun haben, ist die Syntax etwas komplizierter als bei den bisherigen Beispielen.
Der difference Befehl muss vor den Objekten stehen, die voneinander abgezogen werden sollen. Außerdem müssen diese Objekte mit geschweiften Klammern eingefasst werden. Das erste Objekt ist das, von dem das andere Objekt abgezogen wird. Da differnece keine eigenen Parameter hat, bleiben die () leer. Das Ganze sieht dann so aus:
difference() {
cube([65,30,3]);
translate([4,4,-1])cylinder(h=5, d=3.2, $fn = 300);
}
Und als Ergebnis erhalten wir das:
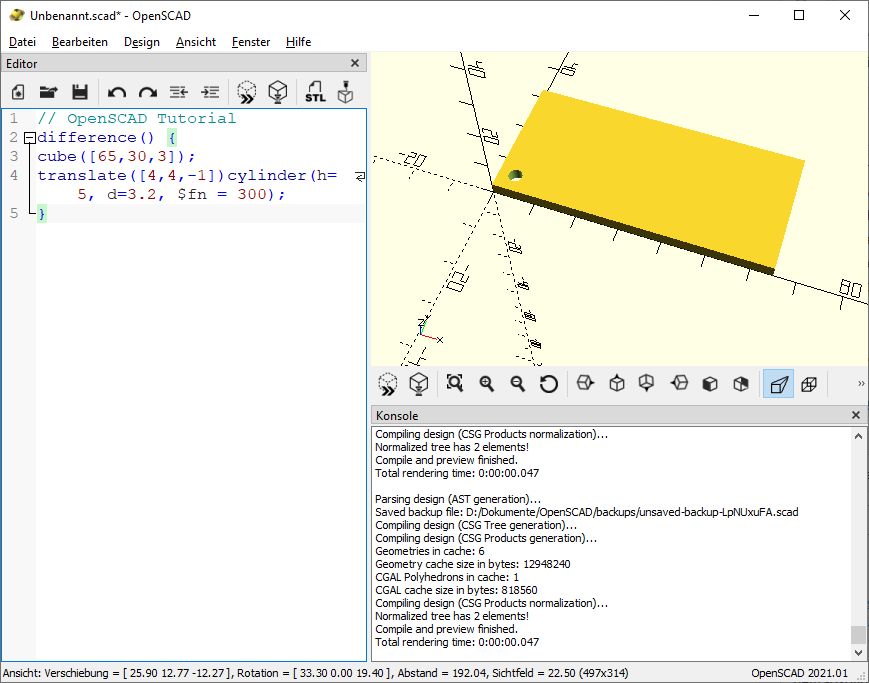
Somit haben wir eine Grundplatte mit einem schönen Schraubenloch darin.
Wir wollen aber nicht nur eine Schraube verwenden, sondern in jeder Ecke eine. Also erzeugen wir nicht nur einen Zylinder, sondern vier. Das kann man blitzschnell mit Kopieren und (dreimal) Einfügen erledigen. Danach muss man nur noch die Koordinaten entsprechend anpassen. Das erste “Loch” hatte jeweils 4 mm Abstand vom Nullpunkt. Das zweite Loch hat in Y Richtung 30 – 4 = 26 mm Abstand. 30 mm ist unsere Grundplatte breit. 4 mm soll der Abstand des Loches sein, also 30 -4 = 26 ist der Wert für die Verschiebung. In X Richtung muss die Verschiebung 65 -4 = 61 betragen. Das vierte Loch bekommt 61 und 26 mm Verschiebung…
difference() {
cube([65,30,3]);
translate([4,4,-1])cylinder(h=5, d=3.2, $fn = 300);
translate([4,26,-1])cylinder(h=5, d=3.2, $fn = 300);
translate([61,4,-1])cylinder(h=5, d=3.2, $fn = 300);
translate([61,26,-1])cylinder(h=5, d=3.2, $fn = 300);
}
Voila, unsere Grundplatte ist fertig:
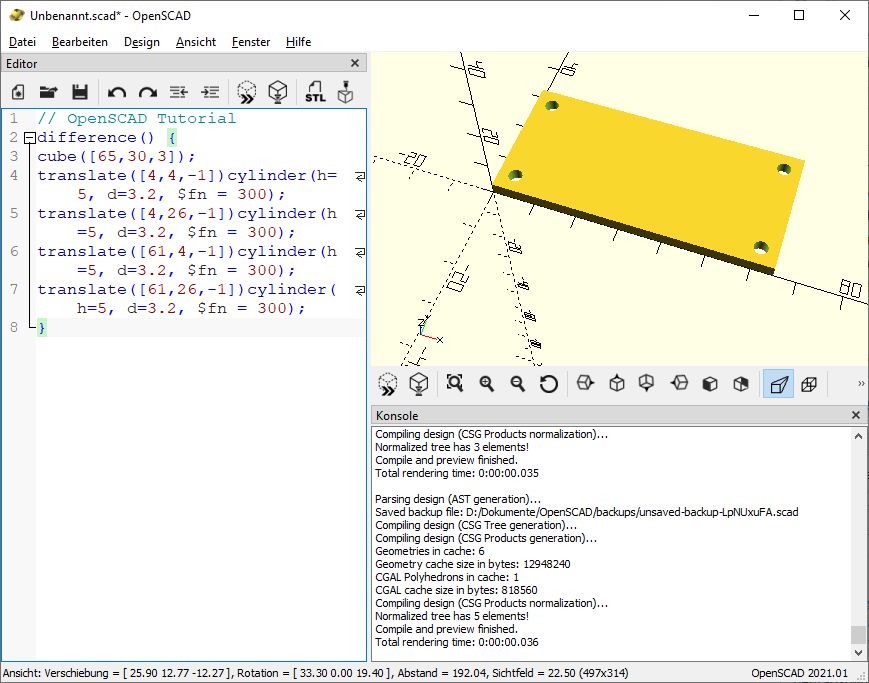
Das ganze ist jetzt schon eine etwas komplexere Operation gewesen. Aber man gewöhnt sich da ganz schnell dran, finde ich.
Hiermit sind die Basics abgearbeitet und wir können im nächsten Teil ernsthaft anfangen, unseren Halter zu konstruieren. Das erfolgt dann im nächsten Abschnitt…